Signed Representation: Two's Complement

1Learning Outcomes¶

Translate between decimal numbers and two’s complement representations
Compare two’s complement to other signed and unsigned representations

🎥 Lecture Video

2Two’s Complement¶

Ones’ complement:

Problem: Negative mappings “overlap” with the positive ones, creating the two 0s.
The solution: Shift the negative mappings left by one.

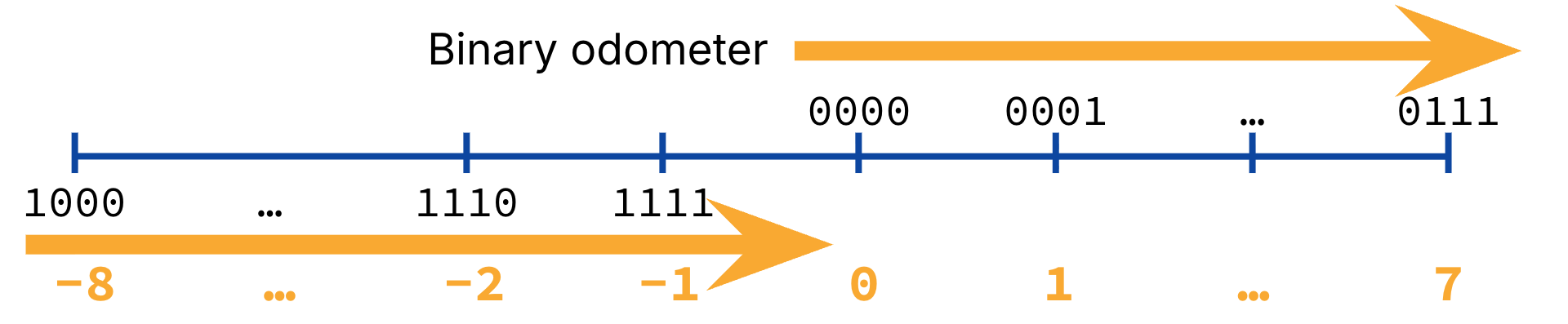
"A blue horizontal number line displays 4-bit binary values and their corresponding decimal equivalents from -8 to 7 to illustrate two's complement representation. Two gold arrows point to the right across the entire scale, indicating that adding to the binary value consistently increases the numerical value across both negative and positive ranges." — Figure 1:“Binary odometer” for 4-bit twos’ complement.

Of note:

Like in ones’ complement, incrementing the binary odometer corresponds with integer addition by one.
0b0000 is still 0.
Positive numbers are the same as ones’ complement.
Negative numbers are shifted over! For example, 0b111 now maps to -1. This gives us one extra negative number.
The most significant bit (leftmost bit) can still be interpreted as the sign bit.

In Two’s Complement, a bit pattern of all ones is -1.

Show Answer

Zero: 1
Positive: $2^{N-1} - 1$
Negative: $2^{n-1}$

3Arithmetic and conversion¶

Hardware for two’s complement is now simple.

Addition is exactly the same as with an unsigned number.

The numbers 5 and -5 are represented in 4-bit two’s complement with 0b0101 and 0b1011, respectively. Adding them together should result in 0, or 0b0000.

"A diagram compares the decimal addition of positive and negative five with the equivalent operation in two's complement binary, adding 0101 and 1011. The binary calculation displays red carry bits and results in a five-bit sum where the leading bit is discarded to achieve the correct four-bit value of 0000, which is the number zero." — Figure 2:Addition in two’s complement follows the decimal intuition.

Explanation

Work right-to-left:

1+1=0 carry 1
1+0+1=0 carry 1
1+1+0=0 carry 1
1+0+1=0 carry 1
1 (is truncated and dropped in 4-bit representation)

(Double check that binary math matches decimal math: $5 + -5 = 0$ )

4Formal definition¶

We can write the value of an $n$ -digit two’s complement number as

- 2^{n-1} d_{n-1} + \sum_{i=0}^{n-2} 2^i d_i

Positive and negative numbers can be computed using the same formula. Above, the sign is computed by multiplying the highest bit by $(-2^{N-1})$ .

Example: 5 and -5 in 4-bit two’s complement

\begin{align} \texttt{0b1011} &= (1 \times –2^3) + (0 \times 2^2) + (1 \times 2^1) + (1 \times 2^0) \\ &= -8 + 0 + 2 + 1 \\ &= -5 \\ \end{align}

\begin{align} \texttt{0b0101} &= (0 \times –2^3) + (1 \times 2^2) + (0 \times 2^1) + (1 \times 2^0) \\ &= 0 + 4 + 0 + 1 \\ &= 5 \\ \end{align}

5Two’s Complement: Flip sign¶

Hardware to convert positive to negative (& vice versa) is simple.

Complement all bits
Then add 1

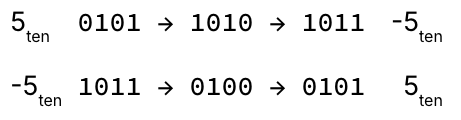
"Two procedures illustrate the two's complement sign-change process by converting positive five to negative five and vice versa. Each example demonstrates flipping the bits of the starting binary value and then adding one to obtain the final result with the opposite sign." — Figure 3:Two’s Complement: To change sign, flip the bits and add one.

At home: Prove algorithm is equivalent to formula!

The intuition comes from a “number wheel” representation of our binary odometer (Figure Figure 4). This wheel also helps us understand identify where integer overflow occurs:

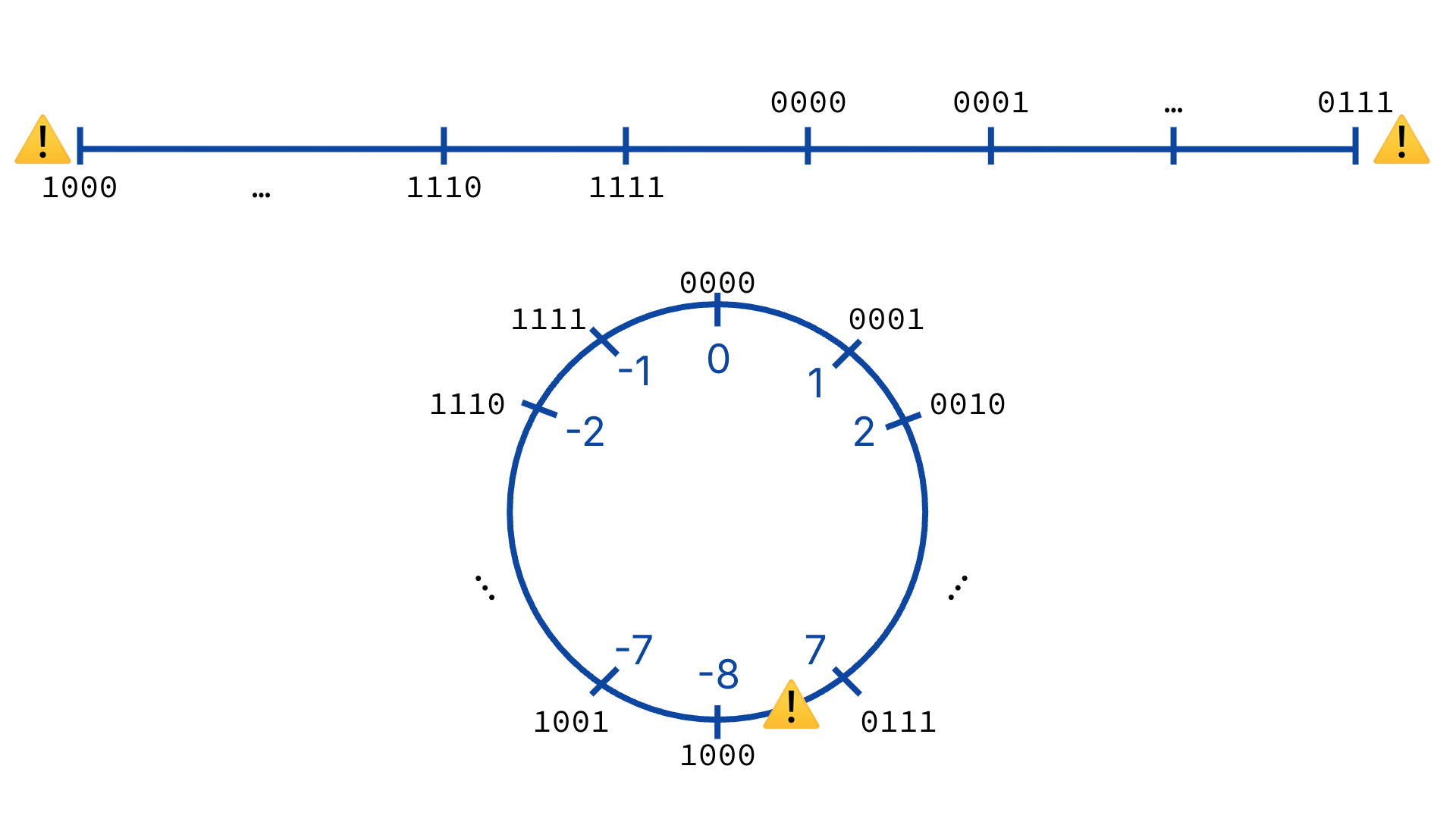
"A horizontal number line and a circular number wheel visually represent the continuity and overflow points of 4-bit two's complement integers. Yellow warning triangles mark the critical boundary between the maximum positive value 0111 and the minimum negative value 1000 to indicate where arithmetic overflow occurs." — Figure 4:Top: A number line indicating where integer overflow occurs. Bottom: A number “wheel” indicating the same integer overflow location.

In Figure 4, 0 through 7 stays the same as it has for every representation. But then it jumps to -8. That cool top-level term (-8) pulls all negative numbers down by one so there is no overlap at zero.

6Two’s Complement: C standard (as of 2025)¶

Two’s complement is the C23 standard number representation for signed integers. Again, the built-in int is ambiguous because it does not specify bitwidth. And again, the header inttypes.h accommodates typedefs like int8_t, int16_t, int32_t, etc., for signed integer representations.