1Learning Outcomes¶
Know the terms: bits, bytes, bitstrings
Compute how many bits you need to represent items.
🎥 Lecture Video
2Digital data¶
Data live all around us.
2.1Example: Storing data as digital¶
The real world is analog—everything you hear and see and smell is all analog. For example, real numbers are a great way to represent the world, but in order for us to use a computer to work with these numbers, we typically need to convert or find equivalent numbers that can be represented digitally.
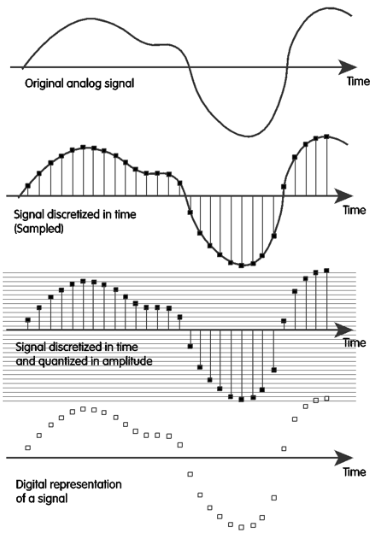
Figure 1:Translating an analog signal to a digital representation.
In order to convert analog data to digital data, we must do two things:
Sample: We ask the signal at every time step: “What’s your value?” This usually occurs at a regular interval. For example, for music on CDs, that’s 44,100 times a second we’re asking it what its height is.
Quantize: Because the height might come out at some fractional number, we need to divide it up in its amplitude using a “yardstick.” We divide it up into a 16-bit number, which is possible tick marks. Then, the sample “snaps” to the closest tick mark.
When we’re all done, we have a set of 16-bit samples that we can work with. There is a lot of engineering that goes into this process. In other classes, you will learn how to sample signals, build analog-to-digital converters, and more. In this class, we focus on designing systems to represent real numbers with a limited number of bits.
2.2Example: Inherently digital data¶
Not all digital data are necessarily boring analog; sometimes you can create art, music, or videos completely without any analog reference. For example, the software POV-Ray is a rendering software that creates beautiful digital images that existed only in the artist’s head. Nowadays, there are entire fields of artificial intelligence around generating digital images and video, often entirely from digital data sources.


3Bits, Bytes, and Nibbles¶
A bit is a binary digit. It takes on the value 0 or 1.
We use the phrases binary string, bitstring, bit sequence, etc. to refer to sequences of binary digits. For example, the set of length-four binary strings refers to the bitstrings 0000, 0001, 0010, ..., 1111.
A byte is a bitstring of length 8. We will find that it is useful to have a standard grouping of bits, so that groups of bits can represent more information. A byte can represent things.
How should we colloquially discuss bytes? Instead of always writing out eight bits (and having to say, “zero zero one zero one one one one” for 00101111), we can write two hexadecimal digits for shorthand (and simply say 2F). Read the next section to learn about how to convert between hexadecimal vs binary values, and why having a hexadecimal shorthand is useful.
If you’re curious, 4 bits is called a “nibble” (or “nybble”) and can represent things. This is equivalent to one hexadecimal digit.
4BIG IDEA: Bits can represent anything!¶
The big idea in this first lecture is:
Bits can represent anything.
Logical Values: Commonly, 0 is false and 1 is true.
Characters: We have 26 characters (A-Z). If we use 5 bits, , so we can have a bit pattern for each character, with six left over for other information.
The ASCII standard is an expanded 8-bit representation that can represent uppercase, lowercase, and punctuation as used in standard American English.
The Unicode standard represents all the world’s symbols and languages, including emojis. There are 8-bit, 16-bit, and 32-bit versions of Unicode.
Colors: HTML color codes are 24-bit (3-byte) representations. Figure 2 shows the HTML color code for California Gold, 0xFDB515. You will read more about hexadecimal and binary in the next section.

Figure 2:HTML Color Codes
Explaining color codes
Revisit this explanation once you’ve read more about hexadecimal and binary in the next section. You can use this example as practice for converting between hexadecimal, binary, and decimal.
FDB515is hexadecimal shorthand (as denoted by the prefix0x) for the bitstring0b111111011011010100010101(as denoted by the prefix0b). We insert spacing below for readability, grouping bits by nibbles:1111 1101 1011 0101 0001 0101These 32 bits are then grouped together into three groups of eight bits to represent the amount of red, green, and blue, respectively, in California Gold. These RGB values are each on a scale of 0 to 255.
Red: “Leftmost” byte,
0xFDor0b11111101or 253.Green: “Middle” byte,
0xB5or0b10110101or 181.Blue: “Rightmost” byte,
0x15or0b00010101or 21.
Locations/Addresses: IPv4 and IPv6 are 32-bit and 64-bit representations of device addresses on the Internet, also known as Internet Procotol addresses. Read more about IP Addreses if you’re curious.
Many types of data You can even represent emotions, like “happy” as 00 or “grumpy” as 01. We note that a 2-bit representation is likely not sufficient for representing the diverse range of human emotions. In fact, attempts to quantify human emotions (often for the purpose of processing data via computers) is a huge area of research. What are the implications of using computers to sample and discretize human experience? For more, we recommend you look into sociotechnical coursework that explores the human contexts and ethics of data.
5Anything you can itemize, you can digitize¶
The big idea of this lecture to memorize:
With N bits, you can represent at most things.
Put another way, you can represent things in at minimum bits, where .
How many bits are needed to represent lowercase letters in English?
There are 26 lowercase letters in the English language: a, b, ..., z.
We therefore need at least 5 bits.
Double check: 5 bits represents things, so we can definitely represent 26 letters (and six other things, if you want). 32 is the smallest power of 2 bigger than the number of things we want to store.
Answer
Answer
Trick question (sorry). We use bits to represent sets of things, not just a single thing. All answers are possible, depending on how many things beyond you are looking to represent.
To use 1 bit, consider representing the two things:
not