Integer Representations

1Learning Outcomes¶

Understand tradeoffs between integer representations:
- (unsigned) integers
- (signed) Sign-Magnitude
- (signed) Ones’ Complement
- Bias Encoding
Identify when and why integer overflow occurs
Perform simple binary operations like addition

🎥 Lecture Video

2Introduction¶

Historically, computers were used as scientific calculators. We therefore dedicate most of our time to understanding how a string of bits (a bit string) can represent a number.

How can we use $N$ bits to represent a set of integers?

There are many systems we can use. Not all systems will help us represent $2^N$ unique integers in $N$ bits! We will focus on representing signed and unsigned integers.

Signed integers refer to positive integers, negative integers, and zero.
Unsigned integers refer to non-negative integers, i.e., at least greater than zero.

3 $N$ -bit Unsigned Integer Representation¶

Let’s get our standard unsigned integer representation out of the way first. The mathematical scheme discussed earlier is sufficient for representing $2^N$ unsigned integers with $N$ bits.

0b0...0 ( $N$ zeros) represents zero
0b1...1 ( $N$ ones) represents $2^N - 1$ (why?)
Everything else: Assume the bitstring is the base-2 representation of a number. Convert.

This representation is supported in C (discussed more later). Built-in types like unsigned int can introduce ambiguity because it doesn’t specify the width of an int. The header inttypes.h accommodates typedefs like uint8_t, uint16_t, uint32_t, etc. to specify unsigned integer representations that are 8-bit, 16-bit, 32-bit etc.

4Design Considerations¶

We will prefer certain systems over others, depending on what sorts of integer operations we want to support.

4.1Common number operations¶

In decimal, we like to add, subtract, multiply, divide, and compare numbers. So we must be able to do the same thing with bit representations of numbers.

It turns out that many arithmetic operations translate reasonably well between decimal and binary.

For example, let’s add 10 and 7, which are 1010 and 0111, respectively, in binary. The result is the number 17, or 10001 in binary.

\begin{array}{rrl} & \texttt{ 11 } & \text{carry bits} \\ & \texttt{ 1010} \\ + & \texttt{ 0111} \\ \hline & \texttt{10001} & \end{array}

Explanation

Work right-to-left:

0+1=1
1+1=0 carry 1
1+0+1=0 carry 1
1+0+1=0 carry 1
1

(Double check that binary math matches decimal math: $10 + 7 = 17$ )

Subtraction in binary works similarly. We leave an in-depth discussion of implementing binary comparison (e.g., $X < Y$ ) to a future project.

4.2The Odometer Analogy¶

In theory, numbers have an infinite number of digits (usually leading zeros), but in computing, we must allocate a finite number of bits. Hardware is limited! Binary bit patterns are therefore abstractions: they are simply representatives of numbers.

In choosing an integer representation, we must consider whether the operations supported will still work within the given bit width of an integer representation. One useful analogy for considering edge cases comes from the idea of an odometer:

Figure 1:A car odometer measures mileage. It starts at 0 and slowly ticks up, then wraps around again. At some point, the odometer above will hit 999999; the next number is again 0.

Two sets of values to consider:

The binary values 000...000, 000...001, 000...010, ..., 111...111
Integers incrementing by one, as placed on a number line

As we will see, there are systems in which the “directions” of these values may diverge.

4.3Integer Overflow¶

Integer overflow: The arithmetic result is outside the representable range of integers.

Suppose we use $N$ bits to represent integers in hardware. If the result of an integer operation ( $+, -, \times, \div, <, =, \leq$ , etc.) cannot be accurately represented in $N$ bits, we say that integer overflow occurred.

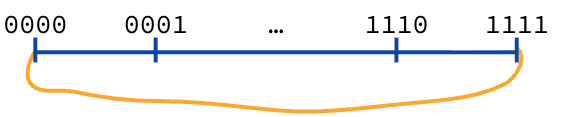
"A blue horizontal line marked with 4-bit binary values from 0000 to 1111 illustrates a finite number system. An gold curved line connects the maximum value back to the minimum value to visually represent the concept of arithmetic overflow in digital systems." — Figure 2:With unsigned integers, the “binary odometer” wraps around.

4-bit unsigned integers: Using 4 bits, you can represent 0 through 15.

Positive Overflow: If you are at 15 (0b1111) and add 1, the value wraps around to 0 (0b0000).
Negative Overflow: If you are at 0 (0b0000) and subtract 1, it wraps around to 15 (0b1111).

4.4 $N$ -bit Signed Integer Representations¶

How do you represent negative numbers? More generally, how do you represent both positive and negative numbers (and zero) with the same $N$ bits?

Sidebar: There was a king who asked his wise thinkers to teach him economics. They kept bringing him long books, and he kept sending them away to make it shorter. Finally, they came back and said, "Sire, we have the theory of economics in four words: ‘Ain’t No Free Lunch.’ " It means you can’t get something for nothing.

If we want to represent negative numbers, you’ve got to give something up; you lose some of the positive numbers you used to have. If we borrow a bit, we can’t go as high in the positive range, but now we can do negatives.

Next, we discuss a few reasonable ones and consider tradeoffs. In the next section, we’ll reveal the standard representation used in modern architectures and supported by the C23 standard.

5Sign-Magnitude¶

Leftmost sign bit: the integer’s sign. 0 is positive; 1 is negative.
Rest of bits: magnitude of the integer in binary

4-bit Sign-Magnitude

Positive numbers: 1 (0b0001) to 7 (0b0111)
Negative numbers: -1 (0b1001) to -7 (0b1111)
Two zeros: +0 (0b0000) and +1 (0b1000)

We already see one problem! With a positive and a negative zero, we’d have to check for two different patterns in code, every time we want to compare values to zero.

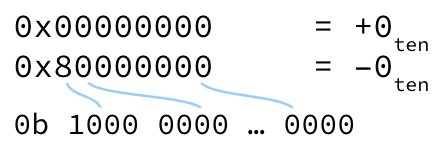
"Two equations display the hexadecimal values 0x00000000 and 0x80000000 equating to positive and negative zero, respectively. Curved lines map the hexadecimal digits to a binary expansion, illustrating that the leading bit determines the sign while the remaining bits represent the magnitude of zero." — Figure 3:Sign-Magnitude has two representations for zero: “positive zero” and "negative zero.

Let’s examine a subtler problem, revealed via the binary odometer:

"A blue horizontal number line displays 4-bit binary values to illustrate sign-magnitude representation, with 0000 at the center. Two gold arrows point in opposite directions from the center to indicate how values increase in magnitude for both positive and negative binary sequences." — Figure 4:“Binary odometer” for 4-bit sign-magnitude.

The problem with Sign and Magnitude is that as the odometer goes up, it goes the wrong way: you go positive, positive, and then suddenly you hit the negative range. Incrementing the binary odometer 0000 to 1111 starts at 0, then 1, through to 7, then wraps to 0 again, then -1, then -7. In other words, sometimes integer addition corresponds to adding bits, and sometimes integer addition corresponds to subtracting bits. This would get complicated very quickly!

Ultimately, Sign-Magnitude is considered a straw man^[1] approach for supporting general purpose computing with integers. Nevertheless, it has some reasonable applications in, say, signals processing, where users are more commonly looking to decouple sign from magnitude, much less add numbers together. Ask us for more.

6Ones’ Complement¶

To represent a negative number, complement the bits of its positive representation.

Here, “complement” means that if the bit is 0 change it to 1, and vice versa. Equivalently, to change the sign of a number, flip all bits of its binary representation.

-7 with 8-bit Ones’ Complement

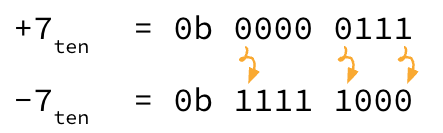
"Two equations demonstrate the ones' complement operation by converting positive seven to negative seven. Curved orange arrows indicate that each bit in the binary sequence `0000 0111` is inverted to produce the resulting sequence `1111 1000`." — Figure 5:Ones’ complement: To change sign, flip the bits.

Start with representing +7: 0b 0000 0111 (we add the spacing and the prefix for better visualization, but the actual bitstring is 00000111)
Flip all bits: 0b 1111 1000 (again, actual bitstring is 11111000) This is the representation of -7.

We’ve fixed one problem. We still get integer overflow, sure, but at least incrementing the binary odometer now corresponds to integer addition by one in most places of the timeline.

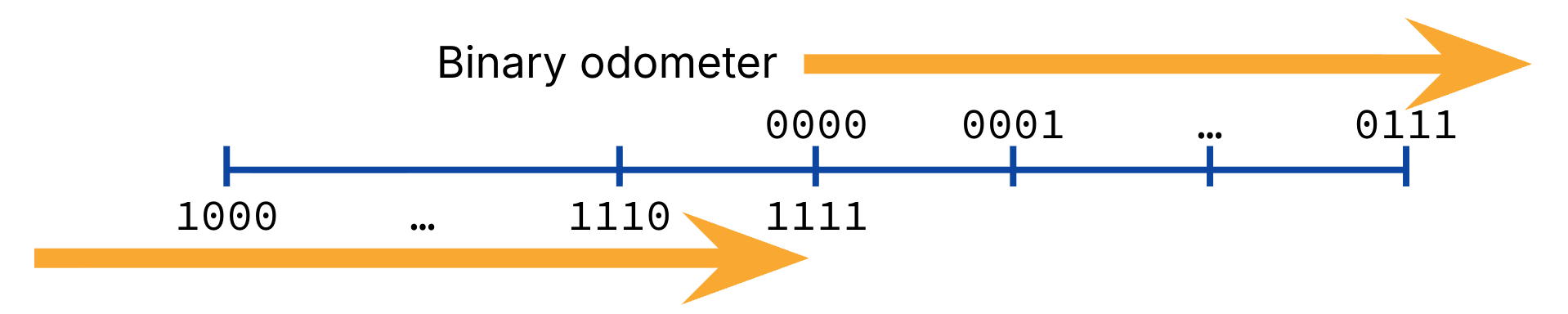
"A blue horizontal number line displays 4-bit binary values to illustrate ones' complement representation, centered around the values 0000 and 1111. Two gold arrows point to the right to indicate that both positive and negative binary sequences increase in value as the odometer increments from left to right." — Figure 6:“Binary odometer” for 4-bit ones’ complement.

Show Answer

Positive numbers: leading 0s
Negative numbers: leading 1s

Show Answer

Zero: 2
Positive: $2^{N-1} - 1$
Negative: (same as positive)

Another added benefit of Ones’ Complement

The leftmost bit (also known as most significant bit) is still effectively the sign bit.

...But we still have the problem of two zeros.

Historically, this was used for a while, but eventually abandoned for two’s complement.

7Bias Encoding¶

Bias Encoding:

Keep track of a bias.
To interpret stored binary: Read the data as an unsigned integer, then add the bias
To store an integer as data: Subtract the bias, then store the resulting number as an unsigned integer.

Imagine you are recording an electrical signal wavering between 0 and 31 volts. Wouldn’t it be cool to grab that graph and pull it down so it wiggles around zero? That’s bias encoding.

We can shift to any arbitrary bias we want to suit our needs. To represent (nearly) as much negative numbers as positive, a commonly-used bias for $N$ -bits is $-(2^{N-1} - 1)$ .

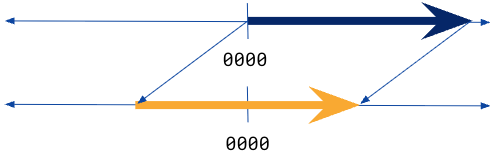
"A diagram presents two parallel horizontal number lines. Vertical lines connect specific points on the top line to corresponding values on the bottom line to indicate the mapping between the two systems." — Figure 7:A bias-encoded representation effectively shifts the number line to an unsigned representation.

Example: $N = 5$ with bias $-(2^{N-1} - 1)$

5-bit integer representation
Bias: $-(2^{5-1} - 1) = 15$
All zeros: smallest negative number The leftmost bit (also known as most significant bit) is still effectively the sign bit.

Here are some diagrams in case they are useful. Figure 8 represents a bias encoding where $N = 4$ and bias $= -7$ . The odometer just does the right thing; it counts up through zero with nothing strange happening.

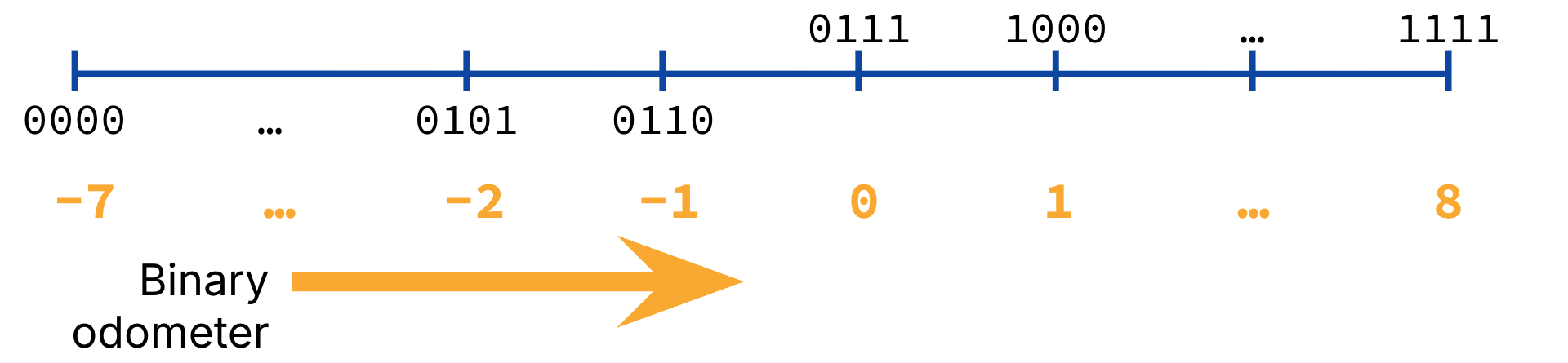
"A blue horizontal number line displays 4-bit binary values and their corresponding decimal equivalents from -7 (for 0000) to 8 (for 1111) to illustrate bias encoding. A single gold arrow points to the right to indicate that the decimal values increase monotonically as the binary sequence increments from 0000 to 1111." — Figure 8:“Binary odometer” for 4-bit bias-encoded integers, with bias -7.

You may also find the number wheel useful for seeing where overflow happens, and how integers increase with respect to binary incrementing. See Figure 9.

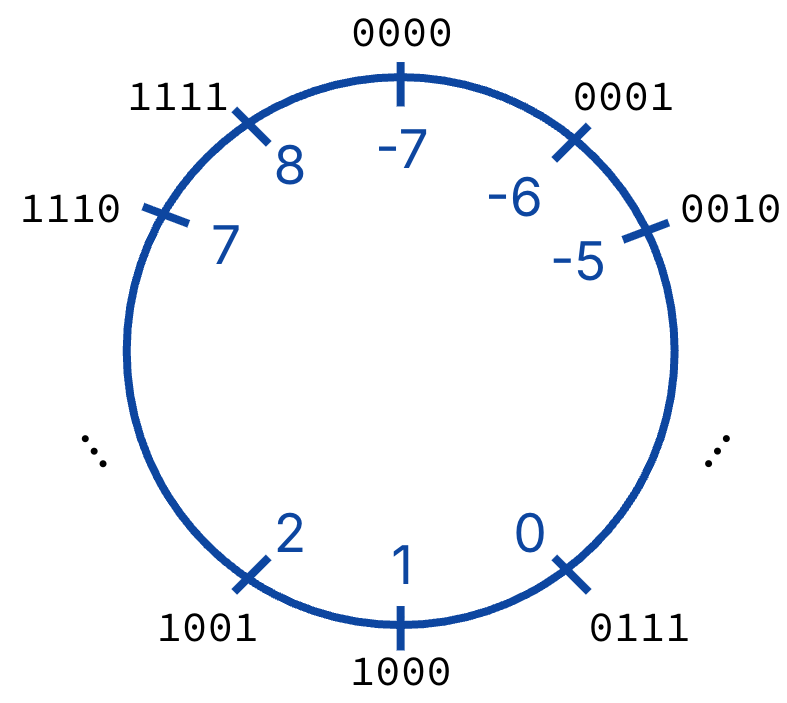
"A circular number wheel visually represents a 4-bit bias-encoded integer. Values inside and outside the wheel represent the numbers and bit representations, respectively; the wheel has tickmarks going from -7 (0000) to 1 (1000) to 8 (1111)." — Figure 9:Number wheel for bias encoding.

We really like biased encoding for some specific applications we’ll see later in the course.

Footnotes¶

Wikipedia: Straw Man
↩